- 스프링정수의 정의
말뚝머리에서 말뚝이 축 또는 축직각방향으로 단위변위량을 발생시키는 축방향력
- 말뚝의 축방향 스프링정수
도로교설계기준해설 p.887 참고
Kv = a (Ap x Ep) / L
Kv : 축방향 스프링 정수 (kN/m)
Ap : 말뚝의 순단면적 (m2)
Ep : 말뚝의 탄성계수 (kN/m2)
L : 말뚝 길이 (m)
a : L/Db에 따른 상수
Db : 말뚝 직경 (m)
| 말뚝 종류 | a |
| 타입말뚝(타격공법) | a = 0.014(L/Db)+0.72 |
| 타입말뚝(바이브로해머공법) | a = 0.014(L/Db)-0.014 |
| 현장타설말뚝 | a = 0.031(L/Db)-0.15 |
| 내부굴착말뚝 | a = 0.010(L/Db)+0.36 |
| 프리보링말뚝 | a = 0.13(L/Db)+0.53 |
| 쏘일시멘트말뚝 | a = 0.040(L/Db)+0.15 |
※ : DRA의 경우 프리보링으로 보는 경우도 있으나 프리보링의 경우 할 경우 값이 더 커지므로 보수적으로 설계하기 위하여 내부굴착말뚝으로 값을 산정
- 말뚝의 축직각방향 스프링정수
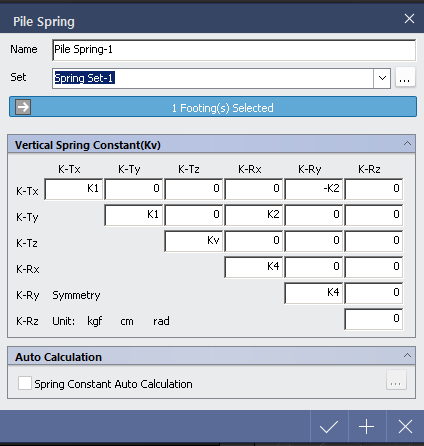
K1, K3 : 말뚝머리부에 회전이 생기지 않도록 하고 말뚝머리부를 말뚝 축직각방향으로 단위량 만큼 변위시킬 때 말뚝 머리부에 작용시켜야 할 축직각방향력 (kN/m) 및 휨 모멘트 (kNm/m)
-> "회전 구속 조건" 횡변위 발생시키는 수평력과 모멘트
K2, K4 : 말뚝머리가 이동하지 않도록 하고 말둑머리를 단위량만큼 회전시킬 때, 말뚝머리가 작용시켜야 할 축직각방향력(kN/Rad) 및 휨 모멘트 (kNm/rad)
-> "수평변위 구속 조건" 회전변위 발생시키는 수평력과 모멘트
토목에서는 일반적으로 반무한 말뚝 (βLe > 3) 말뚝머리 고정 조건이며 h=0 임
위의 조건일 경우
K1 = 4EIβ³
K2, K3 = 2EIβ²
k4 = 2EIβ
여기서
β : 말뚝의 특성치
β = [(kh x Db)/(4EI)]^(1/4)
kh : 수평방향 지반반력계수 (kN/m³)
Db : 말뚝 직경(m)
EI : 말뚝의 휨강성 (E : 탄성계수) (I : 단면 2차모멘트)
수평방향 지반반력계수
kh=(1/30)αE0 x (Bh/30)^(-3/4)
α : 지반탄성계수 산출 방법 및 지반조건에 따라 결정되는 상수
| 다음의 시험방법에 의한 지반탄성계수 E0 (kg/cm2) | α (평상시) | α (지진시) |
| 지름 30cm의 강체원판에 의한 평판재하시험을 반복시킨 곡선에서 구한 지반탄성계수의 1/2 | 1 | 2 |
| 보링공 내에서 측정한 지반탄성계수 | 4 | 8 |
| 공시체의 1축 또는 3축압축시험에서 구한 지반탄성계수 | 4 | 8 |
| 표준관입시험의 N값에서 E0=28N으로 추정한 지반탄성계수 | 1 | 2 |
※ E0 단위 확인 필요
> E0값은 28N을 쓸 경우 매우 큰 값이 나온다. 최인걸 저자의 현장실무를위한 지반공학을 참고하면 토성별 E0값 추정치가 나온다.
Bh : 하중작용방향에 직교하는 기초의 환산재하폭으로서 아래와 같다. 일반적으로 탄성체 기초의 수평저항에 관여하는 지반으로서는 설계지반면에서 1/β까지 고려하면 된다.
직접기초 : Bh = (Ah)^(1/2)
말뚝기초 : bh = (D/β)^(1/2)
E0 : 지반탄성계수
β값 결정 1 (시행착오법) - 구조물기초설계기준 2015 p.347
- β 가정후 E0 값 추정 및 Bh 산정
- kh=(1/30)αE0 x (Bh/30)^(-3/4) 계산
- 2번에서 구한 kh값을 β = [(kh x Db)/(4EI)]^(1/4) 에 대입하여 1번의 β와 비교
- 시행착오법으로 β값 수렴
β값 결정 2 (유도식의 의한 방법)
kh = 1.208(αE0)^1.1 x D^(-0.310) x (EI)^(-0.103)
'토목설계' 카테고리의 다른 글
| 지반조사시 시추심도 기준 (KDS편) (0) | 2023.02.21 |
|---|---|
| 공작물 축조신고 방법 (0) | 2023.02.07 |
| 표토제거(top soil striping) 표준시방 내용 정리 (0) | 2023.01.26 |
| 나라별 콘크리트 강도 시험 비교 (0) | 2023.01.11 |
| Anchor to Anchor 설치 최소 간격 기준 (0) | 2022.09.27 |


댓글